Solutions
Concept:
If f: A → B and g: B → C are functions then g o f (x) = g( f (x)) is a function from A to C.
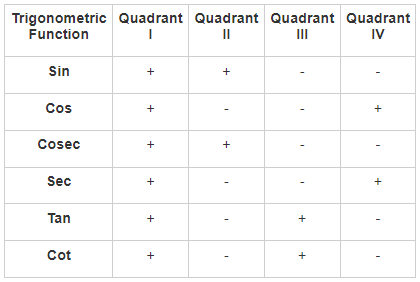
Sign of trigonometric functions in different quadrants is as shown below:
Calculation:
Given: f(x) = |x| and g(x) = cos x
As we know that, if f: A → B and g: B → C are functions then g o f (x) = g( f (x)) is a function from A to C.
So, g o f(3π/4) = g (f (- 3π/4))
∵ f(x) = |x| so, f(- 3π/4) = 3π/4
⇒ g o f(3π/4) = g(3π/4)
∵ g(x) = cos x so, g(3π/4) = cos (3π/4) = cos (π - (π/4))
As we know that, cos (π - θ) = - cos θ
∴ g o f(3π/4) = - cos (π/4) = - √ 2/2------------(1)
Similarly, g o f(5π/6) =g (f (5π/6))
∵ f(x) = |x| so, f(5π/6) = 5π/6
⇒ g o f(5π/6) = g(5π/6)
∵ g(x) = cos x so, g(5π/6) = cos (5π/6) = cos (π - (π/6))
As we know that, cos (π - θ) = - cos θ
∴ g o f(5π/6) = - cos (π/6) = - √3/2---------------(2)
From equation (1) and (2), we get
⇒ g o f(- 3π/4) + g o f(5π/6) = (- √2/2) + (- √3/2)
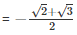



 Get latest Exam Updates
Get latest Exam Updates 





 ×
×






