Solutions
Eight people: A, B, C, D, E, F, G and H.
Years: 1966, 1969, 1977, 1983, 1988, 1993, 2003 and 2008.
Steps:
1) The age of G is a perfect cube.
So, G was born in 1993.
2) The age of D is three times the age of C.
Here, D = 3 × C
51=3 × 17
So, D was born in 1969 and C was born in 2003.
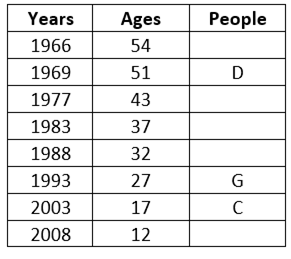
3) The sum of the age of the A and the age of B is a prime number.
So, A+B=54+43=97
Here, two possible cases i.e. case 1 and case 2.
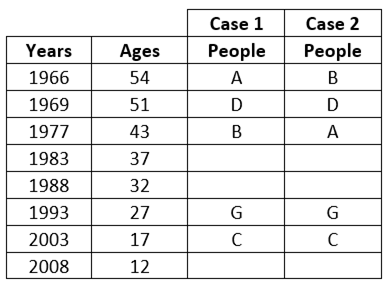
4) The HCF of the age of the H and F is 4.
The prime factorization of 32=25 and the prime factorization of 12=22×31
So, the HCF of 32 and 12=22= 4.
Here, four possible cases i.e. case 1(a), case 1(b), case 2(a) and case 2(b).
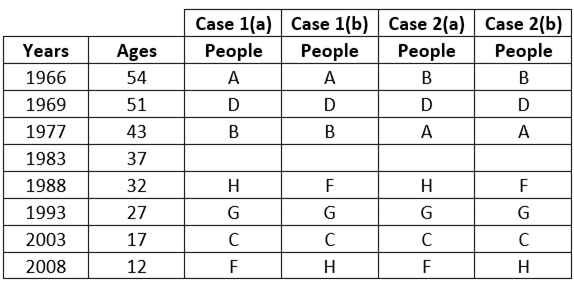
5) The age difference between H and E is 5 years.
Here case 1(b) and case 2(b) get eliminated.
6) B was born just before E.
Here case 2(a) gets eliminated.
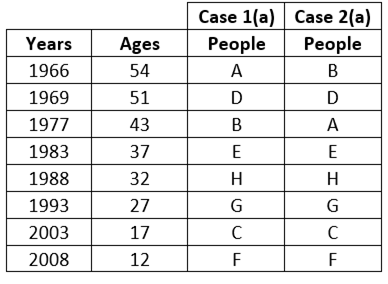
Final arrangement:
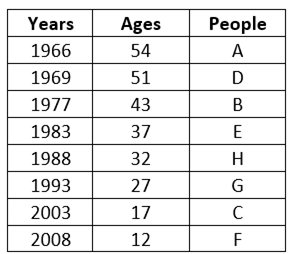
Here, the age of E is 37 years, the age of F is 12 years and the age of C is 17 years.
So, (37+12+17) ÷3=66÷3=22
Hence, 22 years is the average of the age of E, the age of F and the age of C.



 Get latest Exam Updates
Get latest Exam Updates 





 ×
×






