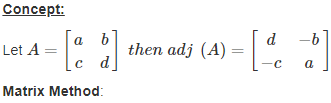
Let us consider the system of linear equations:

a₁₁ × x + a₁₂ × y = b₁

a₂₁ × x + a₂₂ × y = b₂

We can write these equations in matrix form as: A X = B, where

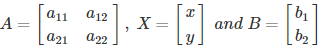
Calculation:

Given: (k + 1) x + 8y = 4k and kx + (k + 3)y = 3k - 1

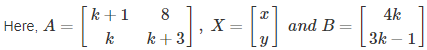
As we know that, for infinite solution |A| = 0 and (adj (A)) × B = O, where O is the null matrix then the system of equations is consistent and has infinitely many solutions.

⇒ (k + 1)(k + 3) - 8k = 0

⇒ k² - 4k + 3 = 0

⇒ k = 1 or k = 3

Now let's calculate (adj (A)) × B

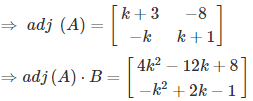
Now by using (adj (A)) × B = O, where O is the null matrix, we get

⇒ 4k² - 12k + 8 = 0 and - k² + 2k - 1 = 0

⇒ k² - 3k + 2 = 0 and k² - 2k + 1 = 0

⇒ k = 1 or 2 and k = 1

So, for k = 1 given system will have infinitely many solutions.

Hence, there are 1 value of k for which the given system will have infinitely many solutions.

Given

Function, y = f(x)

function passes through the point P(2,1)

tangent to the graph y = 3x - 5

Now

equation of tangent of the curve,

y' = mx' + c

where

y' = (3 + c₁) x' + C      ---(iv)

comparing if with tangent to the graph

3 + C₁ = 3

C₁ = 0

C = -5

Since the graph also passes through (2,1) thus

1 = (2 - 1)³ + C₂

C₂ = 0

so, the equation of the graph

y = (x - 1)³

CONCEPT:

CALCULATION:

Given: A kite is flying at an inclination of 60° with the horizontal plane and the length of the thread is 120 m

We have represented the same as in the diagram given below.

In Δ ABC, AB represents the thread i.e AB = 120 m and ∠BAC = 60°

Here, we have to find the height of the kite from the horizontal plane i.e length of side BC.

⇒ BC = 120 ⋅ sin 60° = 60√3 m

Hence, option A is the correct answer.

Calculation:

Given:

The calculation to obtain the value of θ is done as below:

⇒ cos²θ - 3cos θ + 2 = sin²θ

⇒ cos²θ - sin²θ - 3cos θ + 2 = 0

⇒ cos²θ - 1 + cos²θ - 3cos θ + 2 = 0

⇒ 2cos²θ - 3cos θ + 1 = 0

⇒ 2cos²θ - 2cos θ - cos θ + 1 = 0

⇒ 2cos θ(cos θ - 1) - 1(cos θ - 1) = 0

⇒ (cos θ - 1)(2cos θ - 1) = 0

Only statement 'b' is correct.

Hence the correct answer is option 2.

Concept:

• The cross product of vector to itself = 0
• The cross product of collinear vectors = 0
• The dot product of collinear vectors = Product of their Magnitudes

Calculation:

Given:

Concept:

Binomial distribution: If a random variable X has binomial distribution as B (n, p) with n and p as parameters, then the probability of random variable is given as:

P( X = k) = nCk pk (1 – p)(n – k)

Where, n is number of observations.

p is the probability of success & (1 – p) is probability of failure.

k = 0, 1, 2, …., n

Properties:

• Mean of the distribution (μX) = n × p
• The variance (σ2x) = n × p × (1 – p)
• Standard deviation (σx) = √{np(1 – p)}

Calculation:

Hence, option (4) is correct.

Given equation

ax² + bx + c = 0 

x² + x + 1 = 0

both equation has one common root, roots of equation 

x² + x + 1 = 0

Since equation x² + x + 1 = 0 has imaginary roots which always comes in pair

Thus for above two equation, both the roots will be same & all the coefficient will be same

so,

Calculation:

Given:

The equation is  (x + y)dx + (3x + 3y - 4)dy = 0

(4 - 3x - 3y)dy = (x + y)dx

Since y(1) = 0, we get

1 + 3 × 0 + 2log|1 + 0 - 2| = C

⇒ 1 + 0 + 2log|-1| = C

⇒ 1 + 2log1 = C

⇒ C = 1

Hence, the complete equation will be,

x + 3y + 2log|x + y - 2|= 1

Hence, the correct answer is option 1.

Given

Cos θ₁ = 2 cos θ₂

we have to find the value of

as We know

2 Sin A. Sin B = cos (A - B) - cos (A + B)

2 cos A. cos B = cos (A + B) + (A - B)

Thus