There are 4 rows and 4 columns in the above figure. So let n = 4.

Here, we using formulas for finding number of squares in an n × n grid as follows.

Formula :-

n² + (n - 1)² + (n - 2)² + - - - - - - - - - - + (n - n)²

The number of squares in a 4 × 4 matrix is

= 4² + 3² + 2² + 1²

⇒ 16 + 9 + 4 + 1 = 30

Theoretical Method:

To count the square, we will assign a number to each block of the square as shown below:

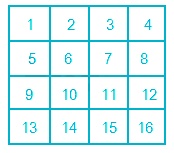
Sqaures involving only one block = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16} = 16 squares

Squares involving four blocks = {(1, 2, 5, 6), (2, 6, 3, 7), (3, 7, 4, 8), (5, 6, 9, 10), (6, 7, 10, 11), (7, 8, 11, 12), (9, 10, 13, 14), (10, 11, 14, 15), (11, 12, 15, 16)} = 9 squares

Squares involving 9 blocks = {(1, 2, 3, 5, 6, 7, 9, 10, 11), (2, 3, 4, 6, 7, 8, 10, 11, 12), (5, 6, 7, 9, 10, 11, 13, 14, 15), (6, 7, 8, 10, 11, 12, 14, 15, 16)} = 4 squares

Squares involving 16 blocks = 1

Total number of squares = 16 + 9 + 4 + 1 = 30 squares.

So, there are 30 squares in the given figure.

Hence, the correct answer is "30".

LOGIC:

In a row inside figures are 5, 3, and 1.

In Row 2:

Squares are 5, 3, and 1.

Hence, option (4) is the correct answer.

The logic followed here is:

Hence, "53" is the correct answer.

5 May 2006 = (2005 years + Period from 1.1.2006 to 5.5.2006)

Odd days in 1600 years = 0

Odd days in 4 years = 0

5 years = (4 ordinary years + 1 leap year) = (4 * 1 + 1* 2) = 6 odd days

31 jan + 28 feb + 31 march + 30 April + 5 may = 125 days

125 days = 17 weeks and 6 days = 6 odd days

Total number of odd days = 0 + 0 + 6 + 6 = 12

12 when divided with 7 we get 5 as remainder.

'5' is the code for Friday.

So, it was Friday on 5 May 2006.

Hence, Friday is the correct answer.

The logic followed here is:

Hirakud, Almatti, and Mettur all are the names of dams.

But Sutlej is the name of a river.

Additional Information

Hence, the correct answer is "Sutlej"

Given Statement -

Anger is an emotion; it needs special skills as to control it.

Assumptions - 

I: Anger need to be controlled - This cannot be considered as an implicit assumption as there is no mention that anger needs to be controlled, it just says controlling it requires special skills.

II: Only skillful people can control it - This is an implicit assumption as can be seen directly through the statements given.

Hence, Option 2 is the correct answer.

The positions of the letters according to the English alphabet series:

Hence, "SV76" is the correct answer.

1. 'Discovery of India' is written by Jawaharlal Nehru.

It is not necessary that Jawaharlal Nehru also the author of "India Wins Freedom".

2. Pandit Motilal Nehru was the father of Jawaharlal Nehru.

Here, the statement does not mention any update regarding the book.

Both the statements together not identify who is the author of "India Wins Freedom"

Hence, "the data given in both statement 1 and statement 2 together are not sufficient to answer the question."

Debating culture gives an opportunity to school children to critically analyse a topic and argue in favour of what they believe in. It prepares them to put forward their ideas and consider the ideas of their opponents. This teaches them to respect and tolerate others’ opinions rather than creating a feeling of resentment. Argument I gives a vague reason as to why debates should not be conducted. Resentment can be caused due to several reasons and not just because of debating. Therefore, option 2 is the right answer.

By using the symbols in the table given below, we can draw the following family tree:

Clearly, the man is the maternal uncle of the woman.

Hence, ‘Maternal Uncle’ is the correct answer.