Concept:

The line of regression of y on x is y - y̅ = byx(x - x̅)

The line of regression of x on y is x - x̅ = bxy(y - y̅)

Calculation:

The line of regression of y on x is y - y̅ = byx(x - x̅)

⇒ x = 5.548 - 0.129y

∴ The two lines of regression are x = 5.548 - 0.129y and y = 6.836 - 0.216x.

Concept:

Calculation:

∴ The regression coefficients byx and bxy are -0.216 and -0.129, respectively.

Concept:

If y = f(x) then slope of the curve at point a is given by y’ = f’(x = a)

Calculation:

Concept:

If y = f(x) then slope of the curve at point a is given by y’ = f’(x = a)

Calculation:

Concept:

If y = f(x) then slope of the curve at point a is given by y’ = f’(x = a).

Calculation:

Concept:

Formulae

Calculation:

Given:

h(x) = 5f(x) – xg(x), where f(x) = x2 - x - 6 and g(x) = x + 10

⇒ h(x) = 5(x2 - x - 6) - x × (x + 10)

⇒ h(x) = 5x² - 5x - 30 – x² - 10x

⇒ h(x) = 4x² - 15x - 30

⇒ h’(x) = 8x - 15.

∴ The derivative of h(x) is 8x - 15.

Explanation:

Referring to the graph for, f(x) =  which is a discontinuous function on [-1, 3] as  it is having an infinite discontinuity at x = 0

So, the fundamental theorem of calculus does not apply to discontinuous functions.

⇒ The value of the integral does not exist.

∴ The correct option is (3).

Given:

Equation of plane P₁ : x + 2y + 3z - 2 = 0

Equation of plane P₂ : x - y + z - 3 = 0 

The plane through the intersection of above planes is at a distance 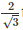 from the point (3, 1, -1)

Concept:

Equation of plane passing through the intersection of two planes P1 and P2 can be assumed as :

P₁ + λP₂ = 0

Formula:

The distance of a point (p, q, r) from a plane ax + by + cz = d is given by :

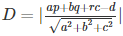
Calculation:

Using P₁ + λP₂ = 0,

Equation of plane through the intersection of above planes is -

(x + 2y + 3z - 2) + λ(x - y + z - 3) = 0      ----      (i)

⇒ (1 + λ)x + (2 - λ)y + (3 + λ)z + (-2 - 3λ) = 0

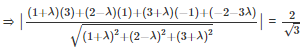
On solving, λ = -7/2

Putting λ = -7/2 in equation (i), we get equation of plane as -

-5x + 11y - z + 17 = 0

⇒ 5x - 11y + z - 17 = 0

∴ a + b + c - 17 = - 22

Concept:

The area of the curve between y = f(x) and y = g(x) {where, f(x) ≥ g(x)} between x = a and x = b is

Calculation:

The area of the region bounded above by y = ex, bounded below by y = x, and bounded on the sides by x =  0 and x = 1 is given by,

Concept:

If p(x) = a₀ + a₁x + …… + anxⁿ, where coefficients of x are real and if an ≠ 0 .Then p(x) is a polynomial of degree n.

Calculation:

Given: f(x) = x² - x - 6 and g(x) = x + 10

Statement I: f[g(x)] is a polynomial of degree 3.

⇒ f[g(x)] = f(x + 10) = (x + 10)² - (x + 10) – 6 = x² + 100 + 20x - x - 16

⇒ f[g(x)] = x² + 19x + 84

⇒ f[g(x)] is a polynomial of degree 2.

Statement I is correct.

Statement II: g[g(x)] is a polynomial of degree 2.

⇒ g[g(x)] = g(x + 10) = (x + 10) + 10 = x + 20

⇒ g[g(x)] is a polynomial of degree 1.

Statement II is incorrect.

∴ Only statement I is correct.