Solutions
A can do a work in 15 days.
B is 25% more efficient than A.
As we know, 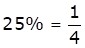
Also, Ratio of efficiency is opposite to ratio of time taken.

According to question:
5x = 15
⇒ x = 3
⇒ 4x = 12
Hence, B can do a work in 12 days.
Let total work = LCM (15,12) = 60 unit
Efficiency of A = 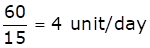
Efficiency of B = 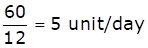
Efficiency of A and B together = 4 + 5 = 9 unit/day
Both work together for 4 days only.
Work finished by them in 4 days = 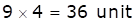
Remaining work = 60 unit – 36 unit = 24 unit
C completed the remaining work in 8 days.
Efficiency of C = 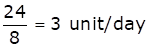
Efficiency of A ,B and C together = 4 + 5 +3= 12 unit/day
Number of days taken by A,B and C to complete the whole work = 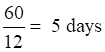



 Get latest Exam Updates
Get latest Exam Updates 





 ×
×






