-
Question 1/30
1 / -0.33
The potential difference measured across a coil is 4.5 V, when it carries a direct current of 9 A. The same coil when carries an alternating current of 9 A at 25 Hz, the potential difference is 24 V. Find the inductive reactance.
-
Question 2/30
1 / -0.33
The sign convention of susceptance is __________ that of the reactance.
-
Question 3/30
1 / -0.33
What is the time constant of the circuit?
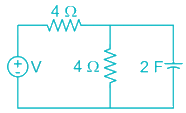
-
Question 4/30
1 / -0.33
A three phase delta load draws _______ power as it would draw when connected as star.
-
Question 5/30
1 / -0.33
An A.C. current is given by i = 100 sin100πt. It will achieve a value of 50 A after_______ second.
-
Question 6/30
1 / -0.33
A voltage e(t) = 100 sin 314 t is applied to series circuit consisting of 10-ohm resistance, 0.0318 henry inductance and a capacitor of 63.6 μF. Calculate impedance of the circuit
-
Question 7/30
1 / -0.33
A balanced star-connected load of (8 + j6) Ω per phase is connected to a balanced 3-phase 400 V supply. Find the line current.
-
Question 8/30
1 / -0.33
The reactance offered by a capacitor to alternating current of frequency 50 Hz is 10 Ω. If frequency is increased to 100 Hz reactance becomes ____ohm.
-
Question 9/30
1 / -0.33
A 3ϕ, star connected balanced load is supplied by 400 V three phase 50 Hz supply. The load takes leading current of
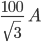
and a power of 20 kW. Find the power factor of the load.
-
Question 10/30
1 / -0.33
Three 100 Ω resistance are connected in star across a 400V 3 ϕ supply. The total power consumed by it is _________.
-
Question 11/30
1 / -0.33
Consider an R-L circuit in which a current i = 10 e-2t A is flowing. The voltage across the RL circuit is given by
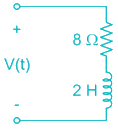
-
Question 12/30
1 / -0.33
Add the following current as vectors:
i1 = 7 sin ωt and i2 = 10 sin (ωt + π/3)
-
Question 13/30
1 / -0.33
A coil having an inductance of 50 mH and resistance 10 Ω is connected in series with a 25 μF capacitor across a 200 V AC supply. Calculate the value of quality factor.
-
Question 14/30
1 / -0.33
The quality factor of an RLC circuit is also known as ______
-
Question 15/30
1 / -0.33
A delta-connected balanced load is connected to 3Φ, 400 V supply. The load PF is 0.8 lagging. The line current is 34.64 ampere. Find the resistance
-
Question 16/30
1 / -0.33
Mathematically a _______ voltage is expressed as V = Vm sin (ωt - ϕ)
-
Question 17/30
1 / -0.33
Rms value is also called as _______ of AC current.
-
Question 18/30
1 / -0.33
A coil having a resistance of 50 ohm and inductances 10 mH is connected in series with a capacitor and is supplied at constant voltage and variable frequency source. The maximum current is 1 A at 750 Hz. Determine the bandwidth.
-
Question 19/30
1 / -0.33
An R-L circuit has Z = (6 + j8) ohm. Its susceptance is _________ siemens.
-
Question 20/30
1 / -0.33
In an alternating circuit, the impressed voltage is given by V = (100 − j50) volts and the current in the circuit is I = (3 – j4) A. Determine the real power in the circuit.
-
Question 21/30
1 / -0.33
A coil of resistance 20 Ω, inductance 0.8 H is connected to a 400 V DC supply. The initial rate of change of current is
-
Question 22/30
1 / -0.33
In a certain application, it is necessary to have a constant time rate of flow of electron i.e. constant current. There a ______is used instead of a ______.
-
Question 23/30
1 / -0.33
For high selectivity, the resistance must be?
-
Question 24/30
1 / -0.33
The conductance is defined as G =
-
Question 25/30
1 / -0.33
A series circuit has R = 10 Ω, L = 0.01 μH and C = 10 μF. Calculate Q - factor of the circuit
-
Question 26/30
1 / -0.33
The projection of a phasor on the Y axis represents _______.
-
Question 27/30
1 / -0.33
Obtaining the voltage, current and power associated with each circuit elements is called as the ____
-
Question 28/30
1 / -0.33
Find the total voltage applied in a series RLC circuit when I = 3 mA, VL = 30 V, VC = 18 V and R = 1000 ohms.
-
Question 29/30
1 / -0.33
A two-element series circuit is connected across an A.C source E = 200√2 sin (ωt + 20°) V. The current in the circuit then is found to be i = 10√2 cos (314 t − 25°) A. Determine the power factor of the circuit.
-
Question 30/30
1 / -0.33
A periodic voltage having the following values for equal time intervals changing suddenly from one value to the next: 0, 5, 10, 20, 50, 60, 50, 20, 10, 5, 0, − 5, −10 V etc. What would be the r.m.s value of sine wave.



 Get latest Exam Updates
Get latest Exam Updates 





 ×
×






