Concept:

Elastic Modulus (E)

When the body is loaded within its elastic limit, the ratio of stress and strain is constant. This constant is known as Elastic modulus or Young's Modulus.

$\mathrm{E}=\frac{\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}{\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}=\frac{\sigma }{ϵ}$

Rigidity modulus (G)

When a body is loaded within its elastic limit, the ratio of shear stress and shear strain is constant, this constant is known as the shear modulus.

$\mathrm{G}=\frac{\mathrm{S}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}{\mathrm{S}\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{r}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}=\frac{\tau }{\varphi }$

Bulk modulus (K)

When a body is subjected to three mutually perpendicular like stresses of same intensity then the ratio of direct stress and the volumetric strain of the body is known as bulk modulus

$\mathrm{K}=\frac{\mathrm{D}\mathrm{i}\mathrm{r}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}}{\mathrm{V}\mathrm{o}\mathrm{l}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{t}\mathrm{r}\mathrm{i}\mathrm{c}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}}=\frac{\sigma }{\frac{\delta \mathrm{V}}{\mathrm{V}}}$

Relationship between E, K and G is:

$\mathbf{E}=\frac{9\mathbf{K}\mathbf{G}}{3\mathbf{K}+\mathbf{G}}$

Other relationship between various elastic constants is:

E = 2G(1 + μ)  

E = 3K (1 – 2μ) 

where μ is Poisson's ratio.

Elasticity of material: The slope of stress-strain curve is known as modulus of elasticity of that material.

Fatigue: Reduction of strength in the material due to cyclic load applied.

Breaking stress of the material: It is the stress at which material fails to resist load.

Energy required to cause failure: Area under stress strain represent energy per unit volume to cause failure.

Explanation:

Maximum shear stress theory

(Guest & Tresca’s Theory)

According to this theory, failure of the specimen subjected to any combination of a load when the maximum shearing stress at any point reaches the failure value equal to that developed at the yielding in an axial tensile or compressive test of the same material.

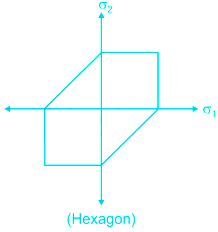
Graphical Representation

${\tau }_{\mathrm{m}\mathrm{a}\mathrm{x}}\le \frac{{\sigma }_{\mathrm{y}}}{2}$ For no failure

${\sigma }_1-{\sigma }_2\le \left(\frac{{\sigma }_{\mathrm{y}}}{\mathrm{F}\mathrm{O}\mathrm{S}}\right)$ For design

σ1 and σ2 are maximum and minimum principal stress respectively.

Here, τmax = Maximum shear stress

σy = permissible stress

This theory is well justified for ductile materials.

Maximum shear strain energy / Distortion energy theory / Mises – Henky theory.

It states that inelastic action at any point in body, under any combination of stress begging, when the strain energy of distortion per unit volume absorbed at the point is equal to the strain energy of distortion absorbed per unit volume at any point in a bar stressed to the elastic limit under the state of uniaxial stress as occurs in a simple tension/compression test.

 for no failure

 For design

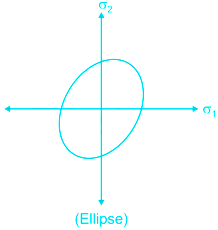
It cannot be applied for material under hydrostatic pressure.

All theories will give the same results if loading is uniaxial.

Maximum principal stress theory (Rankine’s theory)

According to this theory, the permanent set takes place under a state of complex stress, when the value of maximum principal stress is equal to that of yield point stress as found in a simple tensile test.

For the design criterion, the maximum principal stress (σ1) must not exceed the working stress ‘σy’ for the material.

${\sigma }_{1,2}\le {\sigma }_{\mathrm{y}}$ for no failure

${\sigma }_{1,2}\le \frac{\sigma }{\mathrm{F}\mathrm{O}\mathrm{S}}$ for design

Note: For no shear failure τ ≤ 0.57 σy

Graphical representation

For brittle material, which does not fail by yielding but fail by brittle fracture, this theory gives a satisfactory result.

The graph is always square even for different values of σ1 and σ2.

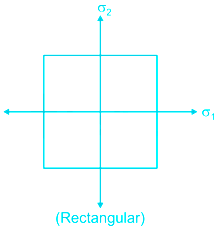
Maximum principal strain theory (ST. Venant’s theory)

According to this theory, a ductile material begins to yield when the maximum principal strain reaches the strain at which yielding occurs in simple tension.

${ϵ}_{1,2}\le \frac{{\sigma }_{\mathrm{y}}}{{\mathrm{E}}_1}$ For no failure in uniaxial loading.

$\frac{{\sigma }_1}{\mathrm{E}}-\mu \frac{{\sigma }_2}{\mathrm{E}}-\mu \frac{{\sigma }_3}{\mathrm{E}}\le \frac{{\sigma }_{\mathrm{y}}}{\mathrm{E}}$ For no failure in triaxial loading.

${\sigma }_1-\mu {\sigma }_2-\mu {\sigma }_3\le \left(\frac{{\sigma }_{\mathrm{y}}}{\mathrm{F}\mathrm{O}\mathrm{S}}\right)$ For design, Here, ϵ = Principal strain

σ1, σ2, and σ3 = Principal stresses   

Graphical Representation

This theory overestimates the elastic strength of ductile material.

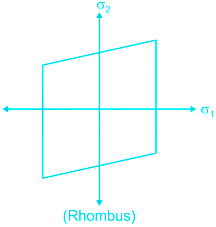
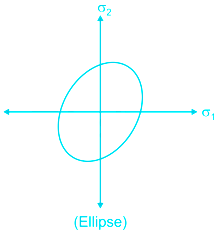
Maximum strain energy theory (Haigh’s theory)

According to this theory, a body complex stress fails when the total strain energy at the elastic limit in simple tension.

Graphical Representation.

  for no failure

 for design

This theory does not apply to brittle material for which elastic limit stress in tension and in compression are quite different.

Concept:

Thermal stress in case of partial expansion:

$\sigma =\frac{\left(\alpha \mathrm{\Delta }\mathrm{T}\mathrm{l}-\delta \right)\mathrm{E}}{\mathrm{l}}$

when temperature increases, induced thermal stress is compressive in nature.

when temperature decreases, induced thermal stress is tensile in nature.

Calculation:

Given:

Length of rod (l) = 2 m = 2000 mm

Coefficient of linear expansion (⍺) = 10 × 10^-6/°C

Young’s modulus (E) = 200 × 10³ MPa

Yield length, δ = 0.2 mm

ΔT = 60 - 20 = 40˚C

Thermal stress in case of partial expansion:

$\sigma =\frac{\left(\alpha \mathrm{\Delta }\mathrm{T}\mathrm{l}-\delta \right)\mathrm{E}}{\mathrm{l}}$

$\sigma =\frac{\left((10\times {10}^{-6}\times 40\times 2000)-0.2\right)}{2000}\times 200\times {10}^3$

σ = 60 MPa (Compressive)

When the temperature of the bar is raised, and the bar is not free to expand, the bar tries to expand and exerts axial pressure on the wall. At the same time wall puts equal and opposite pressure on the bar which will develop compressive stress in the bar.

If there is a drop in the temperature of the bar, the bar will try to contract, exerting a pull on the wall. At the same time, the wall offers equal and opposite reaction exerting a pull on the bar which will develop tensile stress in the bar.

Increase in the temperature → Compressive stress

Decrease in temperature → Tensile stress

If the elongation or contraction is not restricted, i. e. free then the material does not experience any stress despite the fact that it undergoes a strain.

Concept:

Maximum shear stress theory (Guest & Tresca’s Theory)

According to this theory, failure of the specimen subjected to any combination of a load when the maximum shearing stress at any point reaches the failure value equal to that developed at the yielding in an axial tensile or compressive test of the same material.

For no failure

${\tau }_{\mathrm{m}\mathrm{a}\mathrm{x}}\le \frac{{\mathrm{\sigma }}_{\mathrm{y}}}{2}$

For design

${\mathrm{\sigma }}_1-{\mathrm{\sigma }}_2\le \left(\frac{{\mathrm{\sigma }}_{\mathrm{y}}}{\mathrm{F}\mathrm{O}\mathrm{S}}\right)$     $\left\{\because {\tau }_{max}=\frac{{\sigma }_1-{\sigma }_2}{2}\right\}$

where,

τmax = Maximum shear stress

σy = Yield stress

σ1 and σ2 are maximum and minimum principal stress respectively

Calculation:

Given:

σ₁ = 60 MPa, σ₂ = -60 MPa, σ_y = 360 MPa

Now,

${\mathrm{\sigma }}_1-{\mathrm{\sigma }}_2\le \left(\frac{{\mathrm{\sigma }}_{\mathrm{y}}}{\mathrm{F}\mathrm{O}\mathrm{S}}\right)$

$FOS=\frac{{\sigma }_y}{{\sigma }_1-{\sigma }_2}=\frac{360}{60-\left(-60\right)}=\frac{360}{120}=3$

Explanation:

General bending equation is given by:

$\frac{\sigma }{y}=\frac{M}{I}=\frac{E}{R}$

where σ = bending stress at a section, M = Bending Moment at a section, I = Moment of Inertia at a section, E = Modulus of Elasticity for the material of the section, R = radius of curvature

For prismatic bar and pure bending, E, I and M would be constant.

$\therefore \frac{M}{EI}=\frac{1}{R}$

∴ 1/R would be constant and hence R is constant throughout.

Explanation:

Using Superposition theorem,

I: ${\theta }_{B_1}=\frac{P{L}^2}{2EI}$

II: ${\theta }_{B_2}=\frac{ML}{EI}$

${\theta }_{B_1}+{\theta }_{B_2}=0$

$\frac{P{L}^2}{2EI}+\frac{ML}{EI}=0$

$\frac{P{L}^2}{2EI}=\frac{-ML}{EI}$

$M=\frac{-PL}{2}$

So, apply an anticlockwise moment of $\frac{PL}{2}$ at end B₁ so that the total slope at B should be zero.

For a symmetrical ‘I’ section, the intensity of shear stress is maximum at the centroid of the section as shown in the figure.

Concept:

$\tau =\frac{F.A\overline{y}}{b\times I}=\frac{F}{2I}\left(\frac{d^2}{4}-y^2\right)$

Shear stress is zero at the top and bottom fibre (y = d/2)

Shear stress is maximum at a neutral axis (y = 0)

Calculation:

${\tau }_{max}=\frac{F}{2I}\left(\frac{d^2}{4}-0\right)$

$I=\frac{b{d}^3}{12}$

${\tau }_{max}=\left(1.5\right)\frac{F}{bd}$

${\tau }_{avg}=\frac{F}{A}=\frac{F}{bd}=\frac{{\tau }_{max}}{1.5}$

$\frac{{\tau }_{max}}{{\tau }_{avg}}=1.5$

Concept:

The cantilever beam having poooint load at the end is shown in the figure.

The maximum deflection of free end is given as, $\delta =\frac{P{L}^3}{3EI}$

And we know that, the moment equation is, $\frac{\text{M}}{\text{I}}=\frac{\sigma }{\text{y}}=\frac{\text{E}}{\text{R}}$

Calculation:

Given:

L = 2 m, side (a) = 0.1 m, y_max = 5 mm, E = 2.0 × 1011 N/m2.

The maximum deflection

$\delta =\frac{P{L}^3}{3EI}$

$5\times {10}^{-3}=\frac{P\times 2^3}{3\times 2\times {10}^{11}\times I}$

$\frac{P}{I}=375\times {10}^{6}N/m{m}^4$

The moment equation

$\frac{\text{M}}{\text{I}}=\frac{\sigma }{\text{y}}=\frac{\text{E}}{\text{R}}$

${\sigma }_{\text{max}}=\frac{\text{M}}{\text{z}}=\frac{\text{M}\times {\text{y}}_{\text{max}}}{\text{I}}$

${\sigma }_{max}=\frac{375\times {10}^6\times 2\times 0.1}{2}=37.5\times {10}^{6}Pa$

σ_max = 37.5 MPa

Bending equation states that:

$\frac{\sigma }{y}=\frac{M}{I}=\frac{E}{R}$

Various terms in above bending equation are:

σ = Bending stress

y = Distance from neutral axis

M = Bending moment

I = Area moment of inertia

E = Modulus of elasticity

R = Radius of curvature

Concept:

Maximum bending across shaft occurs at either top or bottom fiber and it is given by the bending formula:

${\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{\mathrm{M}}{\mathrm{Z}}=\frac{2\mathrm{M}}{\frac{\pi }{64}{\mathrm{d}}^4}\times \frac{\mathrm{d}}{2}=\frac{64\mathrm{M}}{\pi {\mathrm{d}}^3}$

Maximum shear stress is given by the twisting formula:

${\tau }_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{\mathrm{T}\mathrm{r}}{\mathrm{I}}=\frac{\left(\frac{1}{2}\right)\times \left(\frac{\mathrm{d}}{2}\right)}{\frac{\pi }{32}{\mathrm{d}}^4}=\frac{8\mathrm{T}}{\pi {\mathrm{d}}^3}$

$\frac{{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}}}{{\tau }_{\mathrm{m}\mathrm{a}\mathrm{x}}}=\frac{\frac{64\mathrm{M}}{\pi {\mathrm{d}}^3}}{\frac{8\mathrm{T}}{\pi {\mathrm{d}}^3}}=\frac{8\mathrm{M}}{\mathrm{T}}$

Concept:

The area under the shear-force diagram gives a bending moment between those two points and the area under the load diagram gives shear-force between those two points. i.e.

$M_B-M_A={\int }_A^B{F}_{x-x}dx$

$F_B-F_A=-{\int }_A^B{w}_{x-x}dx$

Calculation:

Given:

$M_C-M_A=\frac{1}{2}\times (14+2)\times 2$

M_C = 16 kN-m   (M_A = 0)

Similarly;

Explanation:

Thermal stress:

• If a rod is heated or cooled, the linear dimensions of the rod get increased or decreased due to the property of the rod i.e. coefficient of linear expansion.
• If the rod is restricted to increase or decrease in dimensions, stress-induced in the bar which is known as thermal stress.
• If the rod is free from any restriction, thermal stress is zero, though strain can be present.
• The thermal stress is given by σt = αEΔT

Composite bar:

• It is a bar or rod with two or three materials.
• The thermal coefficient of expansion of steel (αs) is 12 × 10-6 and the thermal expansion of copper (αc) is 17 ×10-6 (α_c > α_s).
• Being together and of the same length, the strain produced is the same.
• When the composite bar of steel and copper is heated, then the copper member due to its high coefficient of thermal expansion than steel will try to expand more than the steel member but steel due to a lower coefficient of expansion than copper stretched less. Due to this, copper will be in compression while steel will be in tension. 

Concept:

Power in a rotating shaft can be calculated from the equation-

P = ω × T

where $\omega =\frac{2\pi N}{60}$

The relation between shear stress and Torque acting in a shaft can be found by the Torsional equation.

$\frac{\mathrm{T}}{\mathrm{J}}=\frac{{\mathrm{\tau }}_{}}{\mathrm{r}}=\frac{\mathrm{G}\mathrm{\theta }}{\mathrm{L}}$

Calculation:

Given:

d = 2 m, P = 120 W and N = 180 rpm.

We know that

P = ω × T

$P=\frac{2\pi NT}{60}$

$120=\frac{2\pi \times 180\times T}{60}$

$\therefore T=\frac{20}{\pi }Nm$

Using torsional equation

$\frac{\mathrm{T}}{\mathrm{J}}=\frac{{\mathrm{\tau }}_{}}{\mathrm{r}}$

$\tau =\frac{16T}{\pi d^3}$

$\therefore \tau =\frac{16\times \frac{20}{\pi }}{\pi \times 2^3}\Rightarrow \frac{40}{{\pi }^2}N/m^2$

According to Euler’s theory, critical load

$P_{cr}=\frac{{\pi }^{2}EA}{{\left(\frac{kl}{r}\right)}^2}$

Where, A = Cross-sectional area

$\left(\frac{kl}{r}\right)=$ Slenderness ratio.

$\begin{array}{l}\Rightarrow \frac{kl}{r}=\sqrt{\frac{{\pi }^{2}EA}{P_{cr}}}\\ \Rightarrow \left(\frac{k_l}{r}\right)=\sqrt{\frac{{\pi }^{2}E}{f_c}}\end{array}$

Where, $f_c=\frac{P_{cr}}{A}$

Concept:

For a thin cylinder:

(a) Circumferential Stress    (b) Longitudinal Stress

Longitudinal stress: ${\sigma }_L=\frac{pd}{4t}$

Hoop stress: ${\sigma }_h=\frac{pd}{2t}=2{\sigma }_L$

Circumferential or hoop strain (maximum):

${ϵ}_H=\frac{1}{E}\left({\sigma }_H-\nu {\sigma }_L\right)=\frac{{\sigma }_L}{E}\left(2-\nu \right)=\frac{pd}{4tE}\left(2-\nu \right)$

Longitudinal Strain:

${ϵ}_L=\frac{1}{E}\left({\sigma }_L-\nu {\sigma }_H\right)=\frac{{\sigma }_L}{E}\left(1-2\nu \right)=\frac{pd}{4tE}\left(1-2\nu \right)$

Calculation:

Given:

r = 25 cm, d = 50 cm = 500 mm, t = 5 mm, P = 1 MPa, E = 200 GPa = 200 × 10³ MPa, μ = 0.2

${ϵ}_{\mathrm{h}}=\frac{pd}{4tE}\left(2-\upsilon \right)$

${ϵ}_h=\frac{1\times 500}{4\times 5\times 200\times {10}^3}(2-0.2)=2.25\times {10}^{-4}$

Concept:

Deflection of rectangular beam simply supported carrying udl is:

$\mathrm{\Delta }=\frac{5w{l}^4}{384EI}$

$I=\frac{b{d}^3}{12}$

So, from this it is concluded that,

Deflection for the above beam is:

i) directly proportional to its weight

ii) inversely proportional to the cube of its depth

Explanation:

The relation between shear force and load:

The rate of change of the shear force diagram represents the load of that section.

$w=\frac{d\left(s\right)}{dx}$  

where w = load rate and s = shear force.

• The shear force diagram is always one degree higher than the loading diagram hence if we have a point load on the beam then the shear force diagram is constant at all sections.
• If we have two point load on the beam then also shear force diagram is constant but it changes its magnitude suddenly.

• The shear force diagram for the uniformly distributed load is linear.
• The shear force diagram for the uniformly varying load is parabolic.