Solutions
When two or more forces act on a body, they are called to form a system of forces.
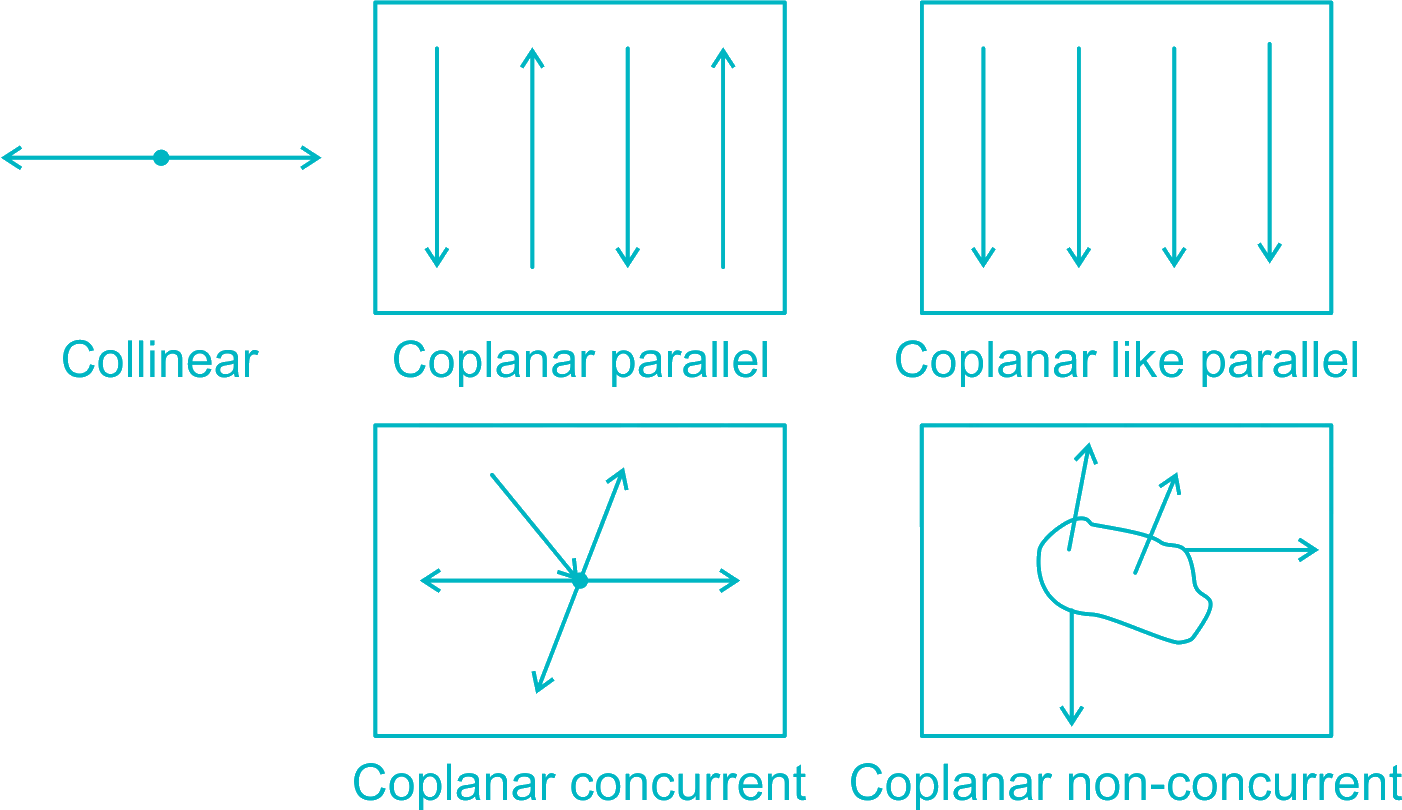
Coplanar forces: The forces, whose lines of action lie on the same plane, are known as coplanar forces.
Collinear forces: The forces, whose lines of action lie on the same line, are known as collinear forces.
Concurrent forces: The forces, which meet at one point, are known as concurrent forces. The concurrent forces may or may not be collinear.
Coplanar concurrent forces: The forces, which meet at one point and their lines of action also lie on the same plane, are known as coplanar concurrent forces.
Coplanar non-concurrent forces: The forces, which do not meet at one point, but their lines of action lie on the same plane, are known as coplanar non-concurrent forces.
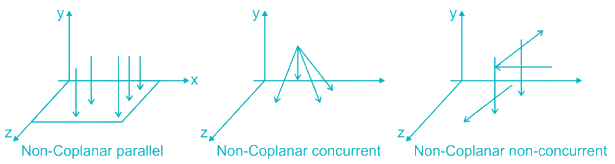
Non-coplanar concurrent forces: The forces, which meet at one point, but their lines of action do not lie on the same plane, are known as non-coplanar concurrent forces.
Non-coplanar non-concurrent forces: The forces, which do not meet at one point and their lines of action do not lie on the same plane, are called non-coplanar non-concurrent forces.



 Get latest Exam Updates
Get latest Exam Updates 





 ×
×






