Let side = x

Draw

As triangle ABC is equilateral triangle.

BE =

BD =

DE = BE – BD =

In triangle ADE by Pythagoras theorem

⇒

⇒  =

⇒

⇒

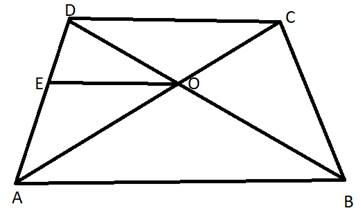
Given :

A trapezium ABCD in which AB∥DC and its diagonals AC and BD intersect at O.

Construction :

Through O, draw EO∥AB, meeting AD at E.

Proof :

In △ADC, EO∥DC

Therefore,

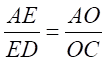⇒ ……………..(1)

In △DAB,EO∥AB

Therefore,

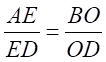⇒  ..........(2)

From 1 and 2, we get,

⇒ ​

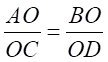
Hence, We can say that The diagonals of a trapezium divide each other proportionally.

Consider second statement :

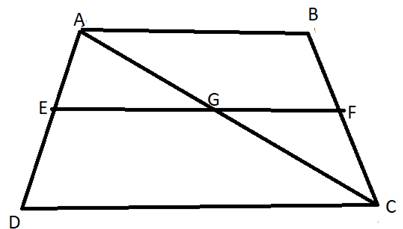
Here, ABCD is a trapezium such that EF||AB||DC

Join EF to cut AC at G.

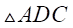 , EG||DC , so by basic proportionality theorem , we have

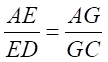⇒ ………………(1)

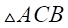 , GF||AB , so by basic proportionality theorem , we have

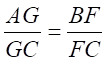⇒ ………………(2)

From (1) and (2)

⇒

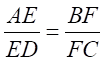
Hence, we can say that Any line drawn parallel to the parallel sides of a trapezium divides the non-parallel sides proportionally.

Hence, both the statements are true.

Assuming roots of the equation  are  and .

Then product of roots =

In triangle BOD,

In triangle OAB,

=

Hence option d is the correct answer.

Let the length of the smaller part becm and the length of the string becm.

Larger part = 4cm

Given that

Wages for 40 women for 30 days = Rs.21,600

Wages for 1 women for 1 day.

But the daily wages for a man is double that of woman.

Hence Wages of man

Number of men

Hence 16 men are required to complete the work in the given frame.

Three taps A,B and C can together fill the tank in 1 hour

Remaining part of the tank

Since C tap is closed so the amount of work needed to be done by (A+B) =

But it has taken them 4 hours to do so.

Hence A and B can together fill the tank in 6 hours.

But we know that

Hence C can alone fill the tank in 6 hours.

SI = (PRT)/100

Hence, SI = (8000×8×8)/100 = Rs 5120

Amount = Principal + Interest

Amount = 8000 + 5120 = Rs. 13120

Difference in the simple interest in 5 years = 2×5 = 10%

Given, 10% of the Amount = Rs 300

Hence, the amount = 300×10 = Rs 3000

Turnover of company Q in May = 48 crores

Turnover of company R in July = 75 crores

Turnover of company T in August = 18 crores

Turnover of company U in June = 55 crores

Required average = (48 + 75 + 18 + 55)/4 = 49 crores

Turnover of company P in June = 48 crores

Turnover of company S in June = 70 crores

Required percentage = [(70 - 48)/70] × 100 = 31.43%

Turnover of company Q and U together in September = 92 + 32 = 124 crores

Turnover of company R and T together in April = 50 + 28 = 78 crores

Required difference = 124 – 78 = 46 crores

Total turnover of all the companies in April = 35 + 38 + 50 + 36 + 28 + 40 = 227 crores

Total turnover of all the companies in May = 45 + 48 + 65 + 58 + 30 + 37 = 283 crores

Total turnover of all the companies in June = 48 + 42 + 46 + 70 + 82 + 55 = 343 crores

Total turnover of all the companies in July = 78 + 58 + 75 + 85 + 65 + 76 = 437 crores

Total turnover of all the companies in August = 23 + 27 + 43 + 25 + 18 + 32 = 168 crores

Total turnover of all the companies in September = 60 + 92 + 28 + 81 + 53 + 32 = 346 crores

Clearly, the maximum turnover is in the month of July.

tan8θ=cot2θ

cot(90⁰−8θ)=cot2θ

90⁰−8θ=2θ

90⁰=10θ

θ=9⁰

tan5θ=tan(5×9⁰)

=tan45⁰=1

cosec(75⁰+θ)=cosec[90⁰−(15⁰−θ)]

=sec(15⁰−θ)

and cot(35⁰−θ)=cot[90⁰−(55⁰−θ)]

=tan(55⁰+θ)

Now cosec(75⁰+θ)−sec(15⁰−θ)−tan(55⁰+θ)+cot(35⁰−θ)

=sec(15⁰−θ)−sec(15⁰−θ)−tan(55⁰+θ)+tan(55⁰+θ)=0

Area of the circular way = 22/7 (3.5²-1.5²) = 31.4 m²

 
                               = 31.4 x 20/100 = 6.28 m³