 176:59 MIN
176:59 MIN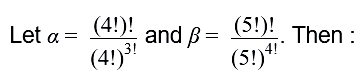
[27-Jan-2024 Shift 2]
All the letters of the word "GTWENTY" are written in all possible ways with or without meaning and these words are written as in a dictionary. The serial number of the word "GTWENTY" IS
[29-Jan-2024 Shift 1]
Number of ways of arranging 8 identical books into 4 identical shelves where any number of shelves may remain empty is equal to
[29-Jan-2024 Shift 2]
In an examination of Mathematics paper, there are 20 questions of equal marks and the question paper is divided into three sections: A,B and C. A student is required to attempt total 15 questions taking at least 4 questions from each section. If section A has 8 questions, section B has 6 questions and section C has 6 questions, then the total number of ways a student can select 15 questions is_____
[30-Jan-2024 Shift 2]
The total number of words (with or without meaning) that can be formed out of the letters of the word 'DISTRIBUTION' taken four at a time, is equal to_____
[31-Jan-2024 Shift 1]
The number of ways in which 21 identical apples can be distributed among three children such that each child gets at least 2 apples, is
[31-Jan-2024 Shift 2]
If n is the number of ways five different employees can sit into four indistinguishable offices where any office may have any number of persons including zero, then n is equal to:
[1-Feb-2024 Shift 1]
The lines L1, L2,...,I20 are distinct. For n = 1, 2, 3,...,10 all the lines L2n−1 are parallel to each other and all the lines L2n pass through a given point P. The maximum number of points of intersection of pairs of lines from the set {L1, L2,...,L20} is equal to :
[1-Feb-2024 Shift 2]
 ×
×